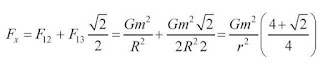Gaya
gravitasi antara dua benda merupakan gaya tarik menarik yang besarnya
berbandinglurus dengan massa masing-masing benda dan berbanding terbalik
dengan kuadrat jarak antara kedua benda.
A. MEDAN GRAVITASI/PERCEPATAN GRAVITASI
Adalah
ruang disekitar suatu benda bermassa dimana benda bermassa lainnya dalam ruang
ini akan mengalami gaya gravitasi.
Keterangan:
F = gaya gravitasi (N)
G = tetapan umum gravitasi (6,67 . 10-9 Nm2 / kg2)
m1 = massa benda 1(kg)
m2 = massa benda 2 (kg)
m = massa benda (kg)
r = jarak (m)
B. HUKUM KEPLER
Hukum kepler ada 3
yaitu :
1. Semua
planet bergerak dengan lintasan elips mengitari matahari dengan matahari berada
di salah satu titik fokusnya.
2.Suatu garis khayal yang menghubungkan matahari dengan planet menyapu luas yang sama dalam selang waktu yang sama.
3. Perbandingan kuadrat periode terhadap pangkat tiga dari setengah sumbu panjang elips adalah sama untuk semua planet.
2.Suatu garis khayal yang menghubungkan matahari dengan planet menyapu luas yang sama dalam selang waktu yang sama.
3. Perbandingan kuadrat periode terhadap pangkat tiga dari setengah sumbu panjang elips adalah sama untuk semua planet.
Keterangan:
T = periode
R = Jarak rata-rata planet ke matahari
CONTOH SOAL :
Jarak rata-rata antara Mars dan matahari adalah 1,52 kali
jarak rata-rata bumi dan matahari, berapa tahun Mars mengelilingi matahari ?
Diketahui :
Sehingga :
C.
GRAVITASI NEWTON
Kita telah membahas tentang massa
dan berat. Masih ingatkah apa perbedaan antara keduanya? Mari kita lihat
kembali ungkapan hukum Newton yang kedua untuk benda yang jatuh ke bawah gaya
yang bekerja pada benda dinamakan gaya gravitasi. Percepatan yang dialami benda
disebabkan oleh gaya gravitasi, sehingga percepatan benda tersebut disebut
percepatan gravitasi. Berapa besanya dan bagaimana arahnya? Mari kita lihat
dulu apa yang disebut sebagai gaya gravitasi.
1. Gaya Gravitasi
 Sedangkan G adalah konstanta gravitasi
universal yang nilainya G = 6,67 u 10-11 N.m2/kg2
. Arah dapat dijelaskan sebagai berikut. Benda kesatu akan mengalami gaya
tarikan ke arah benda kedua dan benda kedua akan mengalami gaya tarikan ke arah
benda kesatu. Besar gaya yang dialami benda kesatu sama dengan gaya yang
dialami benda kedua, yaitu sesuai hukum aksi reaksi. Benda satu memberikan gaya
gravitasi ke benda kedua, benda kedua memberikan reaksi dengan memberikan gaya
gravitasi yang besarnya sama tetapi arahnya berlawanan. Jadi, tanda (-)
menunjukkan kedua massa tarik-menarik.
Sedangkan G adalah konstanta gravitasi
universal yang nilainya G = 6,67 u 10-11 N.m2/kg2
. Arah dapat dijelaskan sebagai berikut. Benda kesatu akan mengalami gaya
tarikan ke arah benda kedua dan benda kedua akan mengalami gaya tarikan ke arah
benda kesatu. Besar gaya yang dialami benda kesatu sama dengan gaya yang
dialami benda kedua, yaitu sesuai hukum aksi reaksi. Benda satu memberikan gaya
gravitasi ke benda kedua, benda kedua memberikan reaksi dengan memberikan gaya
gravitasi yang besarnya sama tetapi arahnya berlawanan. Jadi, tanda (-)
menunjukkan kedua massa tarik-menarik.
1. Medan Gravitasi
Mari kita tinjau sebuah benda bermassa m1
kemudian kita letakkan benda kedua bermassa m2 pada jarak sejauh r.
Gaya gravitasi kedua benda itu dapat dihitung menurut rumus di atas. Benda
kedua akan merasakan gaya gravitasi menuju ke benda pertama. Besarnya gaya
persatuan massa yang dirasakan benda kedua adalah
Gaya gravitasi tiap satuan massa
disebut medan gravitasi.
Tampak bahwa
besar medan gravitasi hanya tergantung pada massa sumber dan jarak.
Misalkan bumi kita
bermassa Mb dari sebuah satelit bermassa m. Benda di sekitar bumi
akan mendapat percepatan gravitasi sebesar , GMb/ r2 atau merasakan medan
gravitasi sebesar itu dengan arah menuju ke bumi. Besar medan yang dirasakan
satelit tidak bergantung pada massa satelit, tetapi bergantung pada kuadrat
jarak antara bumi dan satelit.
CONTOH SOAL :
a. Hitunglah gaya
tarik menarik antara dua benda yang terpisah sejauh 10cm, bila massa masing –
masing benda 5kg!
Penyelesaian :
= 16675 ×
10-11 N
Besarnya gaya tarik – menarik adalah = 16675 × 10-11 N
b. Empat buah massa yang sama sebesar m membentuk sebuah
bujur sangkar berjari-jari R dengan
masing-masing massa terletak disudut bujur
sangkar. Berapakah gaya gravitasi yang dialami massa di salah satu sudut?
Massa 1 juga merasakan gaya karena massa 4 yang arahnya
menuju m4, besarnya gaya
maka gaya gravitasi antara massa 1 dan massa 3 adalah
Arah gaya F12 adalah ke arah sumbu x positif,
arah F14 ke arah sumbu y positif, arah F13 adalah arah
dari massa 1 ke massa 3. Untuk menjumlahkan ketiga gaya tersebut maka F13
yang merupakan besaran vektor kita uraikan ke arah sumbu y dan ke sumbu x.
Total gaya ke arah sumbu x :
Total gaya ke arah sumbu x :
tan Ө =Fy / F, Ө = adalah
sudut antara gaya total F total dengan sumbu x. Karena Fy = Fx
maka sudut yang terbentuk 45o.
D. HUKUM KEPLER
MENURUT NEWTON

Demikian juga dengan hukum Kepler
yang kedua, menurut Hukum Newton gaya yang diberikan oleh matahari pada planet
diarahkan ke matahari. Planet ditarik ke arah matahari, karena arah gaya
sepanjang garis dari planet ke matahari sedangkan arah gerakan tegak lurus
dengan arah gaya maka gaya tersebut tidak memiliki torsi. Akibat tidak memiliki
torsi atau torsinya nol maka momentum sudut planet kekal. Kalian akan
mempelajari kaitan antara torsi dengan momentum sudut pada bab dinamika rotasi.
;
Sebuah planet bergerak mengelilingi matahari.
Dalam waktu dt maka planet bergerak
sejauh vdt dan menyapu luasan sebesar
pada Gambar (2.5), yang merupakan setengah luas jajaran genjang yang dibentuk
oleh vektor posisi r dan v ∆
t
atau besarnya jajaran genjang yaitu dA
adalah r ×
v ∆t . dapat dituliskan sebagai:
Kita nanti akan mengetahui bahwa
besaran r u mv adalah besaran momentum sudut L. Dengan demikian, luas yang
disapu adalah:

Dari persamaan di atas bisa kita
dapatkan:

Mari kita tinjau periode bumi yaitu T. Selama waktu T bumi menempuh perjalanan mengelilingi matahari satu kali putaran penuh,maka jarak yang dilalui adalah keliling lingkaran sebesar 2
Kita masukan persamaan (7) ke persamaan (6) kita mendapatkan
Dan kita akan memperoleh bahwa:
Kita telah mendapatkan hukum
ketiga Kepler. Bagaimana untuk orbit planet yang tidak berbentuk lingkaran?
Bila orbit planet tidak berupa lingkaran tetapi elips maka jari-jari r diganti
jarak rata-rata antara planet dan matahari, yang besarnya sama dengan sumbu
semimayor elips.